ChatGPT for Google Colab
Extension Actions
CRX ID
dfhfeifekpgapdlhfakecbbinnnfoohh
Description from extension meta
Embed ChatGPT inside Google Colab.
Image from store
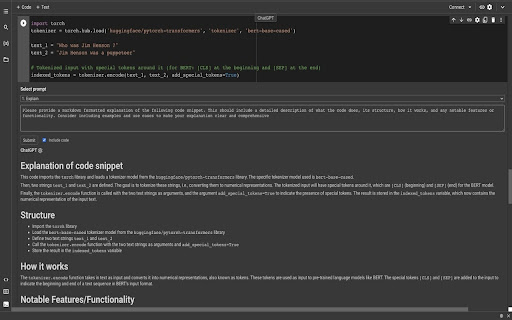
Description from store
This open-source extension provides a user-friendly interface to interact with ChatGPT inside Google Colab. Interact with ChatGPT inside each code cell and save time and effort learning, fixing, and improving your Jupyter notebooks.
Features:
* Free
* Markdown rendering
* Dark, and Light mode
* Copy to clipboard
* All features supported by your ChatGPT account.
* Pre-made prompts for code fixing, refactoring, summarizing, explaining, and adding comments.
* Adapting to newly added code cells.
Source code: https://github.com/ali-h-kudeir/chatgpt-google-colab
Latest reviews
- Cliff C
- Doesn't work: Failed to load response from ChatGPT: Failed to fetch Good idea though
- Mitch y
- such a helpful plugin
- עמוס מרום
- Spectacular. I am a CS/ML teacher and this tools made me 10x more productive.
- Pronoy Sikdar
- Neat utility for developers !
- Jason
- Really helpful! Thank you!
- Mohammad Hossein Hosseini
- when I click on submit I get the following: ``` Failed to load response from ChatGPT: {"detail":"Could not parse your authentication token. Please try signing in again."} ``` However, I found no way to sign in or insert my api-key
- Robert De La Fontaine
- Absolute Gold. I have been looking for a way to incorporate chatGPT into development frameworks that I don't mind coding in. To integrate it this easily, and it still has it's custom instructions, so it feels like I have brought my companion with me, with full knowledge of my Project goals and requirements. Replit also is a great IDE, desktop and cloud based, and it has chatGPT integration through extensions also, which is great. This implementation however, is fantastic. I have only used it for a few minutes so far, but I rate it as "Very Cool". ;
- Luis Alejandro Chanquetti Herrera
- Bien
- Ivan Simsic-Babic
- everything works except for the actual connection to chatgpt, meaning it isnt fetching/moving any data back and forth between colab and chatgpt. this has been the case for over 6 days now, when will this start working again?
- Ivan Simsic-Babic
- everything works except for the actual connection to chatgpt, meaning it isnt fetching/moving any data back and forth between colab and chatgpt. this has been the case for over 6 days now, when will this start working again?
- Justo Fuentes Cuello
- Es excelente ayuda para los estudiantes
- Lalendra Kumar
- This is Awesome tool but since yesterday it not working properly. When i use any features from out of 5. the same prompt shows in output. How to fix this ?
- Lalendra Kumar
- This is Awesome tool but since yesterday it not working properly. When i use any features from out of 5. the same prompt shows in output. How to fix this ?
- DɐtɐX
- Awesome. Makes creating docs wayyy easier. Simple and functional.
- DɐtɐX
- Awesome. Makes creating docs wayyy easier. Simple and functional.
- Cherie Magennis
- Like Stack Overflow on steroids!
- Cherie Magennis
- Like Stack Overflow on steroids!
- 刘尧力
- Awesome!
- 刘尧力
- Awesome!
- Jacopo Ferrero
- simply amazing!!!
- Jacopo Ferrero
- simply amazing!!!
- Hari Lachannagari
- Awesome integration! Thanks Soo Much!
- Hari Lachannagari
- Awesome integration! Thanks Soo Much!
- Thales Souza
- Muito boa, me ajudou em muitos aspectos.
- JiKui Xie
- very good
- JiKui Xie
- very good
- Daniel Cownden
- Such a simple, yet powerful extension to working in notebooks! Is there any way to select which GPT model is being used?
- Daniel Cownden
- Such a simple, yet powerful extension to working in notebooks! Is there any way to select which GPT model is being used?
- Mireia Ribera
- Great for students!
- Mireia Ribera
- Great for students!
- Jayne Jacobs
- You did it, but I knew you would! I keep thinking that by now I should be able to type Latex into a Jupyter notebook and a computer should be able to solve the equation if I state what the variables are. Then it occured to me that you are such a calculator . for example if I give you this problem $\mathbb{P}\left(z \leq -\frac{.44}{1.43/\sqrt{50}} \right) + \mathbb{P}\left(z \leq -\frac{.44}{1.43/\sqrt{50}} \right) = 2\mathbb{P}\left(Z\leq - 2.175\right)$ you can tell me the value of $\mathbb{P} It seems like you have a probability-related problem involving the standard normal distribution, and you want to find the value of $\mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}}) + \mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}}) = 2\mathbb{P}(Z \leq - 2.175)$, where $z$ is a standard normal random variable and $Z$ is another standard normal random variable. Let's solve this step by step: Step 1: Calculate the probability value for the left-hand side of the equation. We need to calculate $\mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}}) + \mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}})$. Step 2: Calculate the probability value for the right-hand side of the equation. We need to find $2\mathbb{P}(Z \leq - 2.175)$. Step 3: Compare the results of Step 1 and Step 2. Let's proceed with the calculations: Step 1: To calculate $\mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}})$, we need to find the cumulative probability for the standard normal distribution. Using a calculator or a statistical software, we find that $\mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}}) \approx 0.003139$. Step 2: Next, we calculate $2\mathbb{P}(Z \leq - 2.175)$. Again, using a calculator or a statistical software, we find that $2\mathbb{P}(Z \leq - 2.175) \approx 0.03025$. Step 3: Finally, we compare the values from Step 1 and Step 2: $0.003139 + 0.003139 \approx 0.006278$ (rounded to 6 decimal places) The value $0.006278$ does not equal $0.03025$, which means the equation $\mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}}) + \mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}}) = 2\mathbb{P}(Z \leq - 2.175)$ is not valid. If there's anything else you'd like to know or if you have additional questions, feel free to ask!
- Jayne Jacobs
- You did it, but I knew you would! I keep thinking that by now I should be able to type Latex into a Jupyter notebook and a computer should be able to solve the equation if I state what the variables are. Then it occured to me that you are such a calculator . for example if I give you this problem $\mathbb{P}\left(z \leq -\frac{.44}{1.43/\sqrt{50}} \right) + \mathbb{P}\left(z \leq -\frac{.44}{1.43/\sqrt{50}} \right) = 2\mathbb{P}\left(Z\leq - 2.175\right)$ you can tell me the value of $\mathbb{P} It seems like you have a probability-related problem involving the standard normal distribution, and you want to find the value of $\mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}}) + \mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}}) = 2\mathbb{P}(Z \leq - 2.175)$, where $z$ is a standard normal random variable and $Z$ is another standard normal random variable. Let's solve this step by step: Step 1: Calculate the probability value for the left-hand side of the equation. We need to calculate $\mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}}) + \mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}})$. Step 2: Calculate the probability value for the right-hand side of the equation. We need to find $2\mathbb{P}(Z \leq - 2.175)$. Step 3: Compare the results of Step 1 and Step 2. Let's proceed with the calculations: Step 1: To calculate $\mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}})$, we need to find the cumulative probability for the standard normal distribution. Using a calculator or a statistical software, we find that $\mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}}) \approx 0.003139$. Step 2: Next, we calculate $2\mathbb{P}(Z \leq - 2.175)$. Again, using a calculator or a statistical software, we find that $2\mathbb{P}(Z \leq - 2.175) \approx 0.03025$. Step 3: Finally, we compare the values from Step 1 and Step 2: $0.003139 + 0.003139 \approx 0.006278$ (rounded to 6 decimal places) The value $0.006278$ does not equal $0.03025$, which means the equation $\mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}}) + \mathbb{P}(z \leq -\frac{0.44}{1.43/\sqrt{50}}) = 2\mathbb{P}(Z \leq - 2.175)$ is not valid. If there's anything else you'd like to know or if you have additional questions, feel free to ask!
- Shashank Badgujar
- Amazing !!!
- Shashank Badgujar
- Amazing !!!
- Anonymous
- Awesome integration! Thanks Soo Much!
- Ani Verzivolli
- Writting code in google colab just became easy. Much more useful built-in as to ask chat and copy paste from a page to another
- Ani Verzivolli
- Writting code in google colab just became easy. Much more useful built-in as to ask chat and copy paste from a page to another
- Yura Pylypchuk
- LOVE IT!
- Yura Pylypchuk
- LOVE IT!
- Messian
- nice job
- Messian
- nice job
- Ali Farki
- Amazing
- Ali Farki
- Amazing
- Mordecai Brian
- Awesome...just awesome
- Mordecai Brian
- Awesome...just awesome
- Shashank Badgujar
- Amazing extension .!! Error solving made easy :)
- Shashank Badgujar
- Amazing extension .!! Error solving made easy :)
- Shumin Zheng
- This tool is great, you don't have to leave Colab (except for the first time in a while you need to log in to your ChatGPT account). I also like the built-in prompts for common types of questions you might want to ask, save a bunch of time.
- Shumin Zheng
- This tool is great, you don't have to leave Colab (except for the first time in a while you need to log in to your ChatGPT account). I also like the built-in prompts for common types of questions you might want to ask, save a bunch of time.
- kai algo
- it would be better if it could only explain selected code, not whole cell. but thanks.